Chapter6 week11

[實做筆記區]

※6.1 Interpolation of Data
Start with a simple problem:suppose we have a collection of four values that we wish to enlarge to eight.

「如何把四個數字擴大八個數字？」
　在6.1中一共提到了四個方法，
　而Figure6.1與6.2指的是同一種方法...

「Slightly redrawn」 (Page.120)
　X1 ~ X4 之間一共有三個間隔，而每個間隔相差的直為1
　X'1 ~ X'8 的長度與 X1~X4的長度相等，此外
　X'1 ~ X'8之間一共有七個間隔，每個間隔的大小為3/7 也就是0.4286

　數學公式如下：X'=1/3(7x-4)
　　　　　　　　X =1/7(3x'+4)

「Nearest-neighbor interpolation」 (Page.120)
　X →X' 挑最近的的點 如6.3所示
　X1最近的點：X'1 ＆ X'2 (課本於X'2標空圈)
　X2最近的點：X'3 ＆ X'4
　X3最近的點：X'5 ＆ X'6
　X4最近的點：X'7 ＆ X'8 (課本於X'7標空圈)
「Linear interpolation」 (Page.121)
　F-f(X)/λ = f(X2)-f(X1)/1
　→F=λf(X2)+(1-λ)f(X1)
　註：F是想知道的X'n
　　　λ是以 X1 到 X2 的距離，F距離 X1 佔整段比例的比數

---

　
※6.2 Image Interpolation
　6.1提到了點與線之間的數值放大(使用線性做範例)
　6.2則是一個面的，也就是Image。
　Example：將4×4的Image放大到8×8
　(x,y)對應到放大後的位置，用下面的公式計算
　該公式稱為 bilinear interpolation
　f(x',y')=λμf(x+1,y+1)+λ(1-μ)f(x+1,y)
　　　　　+(1-λ)μf(x,y+1)+(1-λ)(1-μ)f(x,y)

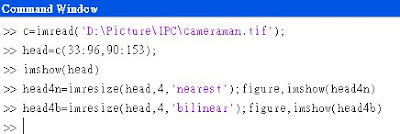
　Matlab內有個function叫做 imresize 負責上述提過的處理
　語法是：resize(A, k, 'method')
　method一共有：'nearest', 'bilinear', 'bicubic' 三種方法

---

※6.3 General Interpolation (Page.125)
　本節提到的是cubic interpolation
　也就是Method中的bicubic....
　f(x')=R3(-1-λ)f(x1)+R3(-λ)f(x2)+R3(1-λ)f(x3)+R4(2-λ)f(x4)
　x'透過 x1, x2, x3, x4 共四個點計算出
　解讀如下：
　因為計算的過程中該曲線f(x) x值 最高項次是 3次方
　此外，在平面上求得(x',y')需仰賴bilinear的概念
　故稱為bicubic interpolation

---

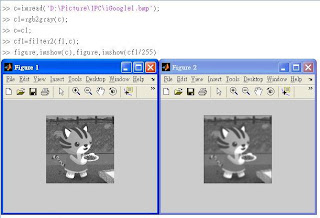
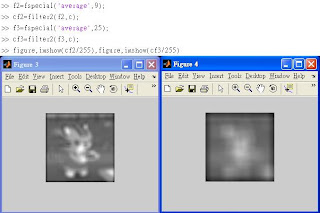
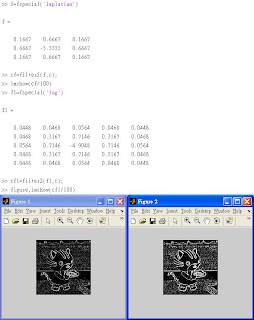
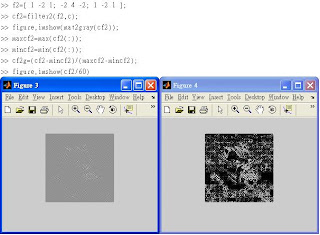
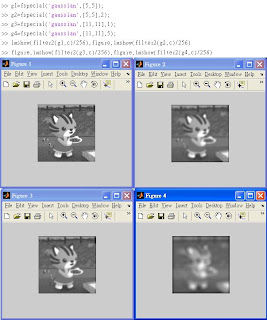
※6.4 Enlargement by Spatial Filtering　
　在Enlarge的過程中使用filter(?)

---

※6.5 Scaling Smaller
　似乎可以用公式畫圓(但是沒有成功= =)

---

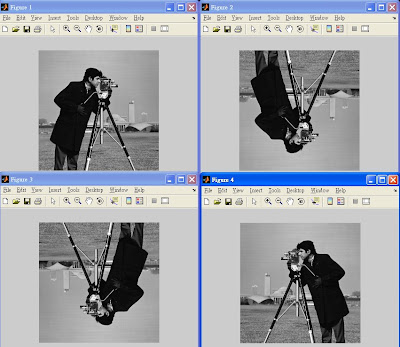
※6.6 Rotation (旋轉)
　將圖片(中的每個點)旋轉Θ度
　語法如下：var = imrotate(c,60);
　　　　　　//將c旋轉60度的值給var
　此外，旋轉90度的倍數有特殊的語法
　 90度：c90 = flipud(c);
　180度：c180 = filplr(flipud(c));
　270度：c270 = fliplr(c);

---

※6.7 Anamorphosis (失真圖像)

---

[問題區]
1.　Page 120, Figure 6.3
　　Nearest-neighbor interpolation，以空圈標記了最近的點
　　然而位於邊緣的 X1 ,與 X4 僅僅標記了X'2與X'7
　　X'1與X'8並未被標，是因為重疊的關係？

　　在這張圖，從 X'→X 似乎沒有太大的問題
　　　　　然而從 X→X' 是否如字面意義挑最近的點
　　例如 X'3 較 X'4更接近 X2...X→X'時，X2是否取X'3的值

2.　Page 137
　 90度：c90 = flipud(c);
　180度：c180 = filplr(flipud(c));
　270度：c270 = fliplr(c);

　因為課本上使用imrotate的旋轉，是逆時鐘旋轉...
　然而這邊提到特殊與法的時候，有提到度數
　我以為c90的結果應該與imrotate(c,90)相同
　然而實際上並不是，而是往下折(x,y')

　c180 也不等於 imrotate(c,180)而是(x',y')　
　c270 是(x',y)

　註：(x,y')是指 x 相對位置不變，y的位置作映射
　　　(x',y') x y 作映射
　　　(x',y)是指 y 相對位置不變，x的位置作映射

　這樣算是我解讀上有所問題嗎？

期中報告 notes

3. [ 注意 ] 請同學撰寫一份期中報告, 繳交至 Homework Show @ IPC, 內容為描述自己在本課程前半學期的學習情形, 回顧自己哪方面表現不錯? 哪方面需要加強? 老師應加強哪些課程內容? 最後, 給自己的學習打成績。第 11 週課程我們將進行課程期中回顧。

筆記筆記筆記....囧

待續XD

[學習情形]
每週都有按照老師規定的進度好好的閱讀與實做
除了3.6(如果沒記錯)那次沒有跟上外

[自認不錯]
有試著使用blog做閱讀紀錄，
方便將來回顧時使用。

[尚待加強]
上課學過的東西，或許當下聽懂了，
然而有部分機率在不久後將之遺忘。

[課程內容]
本身對於課程內容與上課方式並沒有任何疑問

[自我評分]
80

雖然有使用blog做紀錄，然而紀錄卻不是那麼的詳細
有時因為偷懶而缺記的，還得重新翻書才會有印象

提問題，總覺得有一些是可以自行解決的...
提問題之後，或得解答也未必即時更新blog
有時問題提過後，部份沒獲得解答的問題就此閒置

就努力實作與閱讀方面，覺得應該有超過80分的門檻
但是因為後續偷懶方面的小瑕疵，自認該扣分...

Week7 Homework7

※閱讀心得－－以下以章節與頁數呈現

※5.1 Introduction
[Page 89]
Spatial filtering thus requires three steps:
1. Position the mask over the current pixel.
2. Form all products of filter elements with the corresponding elements of the neighborhood.
3. Add all the products.
↑This must be repeated for pixel in the image. (!!!!)
關於我的解讀：
1. 先選出想要的current pixel
2. 列出他的Pixel Neighborhood
3. 選定他是Mask的範圍
4. 將週遭的Neighborhood乘上特定乘積並加總在current pixel的位置
5. 輸出

[Page 90]
magic(N)就是楊建貴教授以前敎過的魔術方塊
N是決定他的大小：N×N大小的矩陣

↑分別是乘以10之後與之前

課本將之乘以10倍的大小
關於Page 90與Page 91的程式範例，有誤導的錯覺
因此自製了一些對照圖：







※5.3 Filtering in MATLAB
Y = filter2(B,X,'shape')
'same'-原本的大小 (原本是5×5的話)
'valid'-compute without the zero-padded(會變3×3)
'full'- 把邊緣也用特殊算法填滿(7×7)
使用圖片對照應該會更加清晰，如下：
◎使用same
◎使用valid

◎使用valid時若補零(※詳見5.2.1 Pad with zeros.)，會出現與same效果相等的結果

◎使用Full的效果(框線內是為了跟same做比較)


Page 95
fspecial('average',[5,7])→矩陣的element都是0.286(總和為1)
fspecial('average',11)→矩陣內的element都是0.0083(總和為1)
◎程式碼demo如下(3x3大小的filter)：


◎同上，改用9x9與25x25的filter：



關於Functio "fspecial"，Page 98用到fspecial('')
'laplacian' filter approximating the 2-D Laplacian operator
'log'　　　　Laplacian of Gaussian filter
'gaussian'　Gaussian lowpassfilter
註：laplacian又叫做「拉普拉斯」
◎Page 98的程式結果如下：


Page 101 =>High-pass filters are often used for edge detction.
◎Page 101-Scaling transformation.

↑據說右邊那個圖，High-pass filters are often used for edge detection. The picture can be seen quite clearly.

※5.5 (未細讀)
關於「Gaussian Filter」
◎但是下圖展示關於Gaussian的效用：


※5.7 Nonlinear Filters
→maximum filter
→minimum filter
→rank-order filter
the mini filter is a rank-order filter for which the first element is returned,and the maximum filter is a rank-order filter for which the last element is returned.

Use function "nlfilter"


※問題區
1.　Page 93,94
　　關於filter2的"same","valid","full"，
　　課本有些簡單的範例，例如在x的四周補0後使用"valid"的效果
　　與直接使用"same"的效果相同
　　知道每個單字出現的範圍大小，但實際計算方式仍不太了解
　　→已知課本範例結果"valid"3×3,"same"5×5,"full"7×7

2.　Page 96,97 5.3.1
　　關於「Separable Filters」
　　示範把陣列分離成1×N與N×1
　　並提到Separability can result in great time savings.
　　關於這邊，語句上的翻譯是節省時間
　　而關於節省，到底是節省怎樣的時間？
　　抑或是節省記憶體的空間呢？(是否有此項功能)

3.　Page 99 Figure 5.5 的解說
　　In each case, the sum of all filter element is zero.
　　意指，構成上述圖片的fliter元素相加總合為0
　　在網路上搜尋了關於Laplacian的事蹟，
　　或許這問題不是很重要，但仍然好奇該矩陣是如何構成？

4.　Page 108 (應該放到課本找錯區嗎= =?)
　　f=[-1 -1 -1;-1 11 -1; -1 -1 -1]/9;
　　xf=filter2(x,f);
　　imswho(xf/80)
　　根據上述指令操作，只有出現一個小點(約3×3大小)
　　但當我將xf=filter2(f,x); //x與f的位置對調
　　就可以show出圖片大小的圖

5.　Page 111(應該放在課本找錯區)
　　假設有一張圖片存在x裡面
　　原本→cmax=nlfilter(c,[3,3],'max(x(:))');會不能用
　　修改→cmax=nlfilter(x,[3,3],'max(x(:))');才能用
　　→cmin亦同
　　但當我將一張圖片大小與x相同的圖片塞到c裡
　　就可以用課本上的指令，那麼該算是筆誤還是？
　　如此一來，是否意指cmax=nlfilter(x,[3,3],'max(x(:))');前後變數該相同？



※專業術語問題區
1.　high-boost filter = 高xx濾波器？
　　同上，high-pass filter = 高xx濾波器？

2.　geometric mean filter

3.　alpha-trimmed mean filter

4.