Week7 Homework7

※閱讀心得－－以下以章節與頁數呈現

※5.1 Introduction
[Page 89]
Spatial filtering thus requires three steps:
1. Position the mask over the current pixel.
2. Form all products of filter elements with the corresponding elements of the neighborhood.
3. Add all the products.
↑This must be repeated for pixel in the image. (!!!!)
關於我的解讀：
1. 先選出想要的current pixel
2. 列出他的Pixel Neighborhood
3. 選定他是Mask的範圍
4. 將週遭的Neighborhood乘上特定乘積並加總在current pixel的位置
5. 輸出

[Page 90]
magic(N)就是楊建貴教授以前敎過的魔術方塊
N是決定他的大小：N×N大小的矩陣

↑分別是乘以10之後與之前

課本將之乘以10倍的大小
關於Page 90與Page 91的程式範例，有誤導的錯覺
因此自製了一些對照圖：







※5.3 Filtering in MATLAB
Y = filter2(B,X,'shape')
'same'-原本的大小 (原本是5×5的話)
'valid'-compute without the zero-padded(會變3×3)
'full'- 把邊緣也用特殊算法填滿(7×7)
使用圖片對照應該會更加清晰，如下：
◎使用same
◎使用valid

◎使用valid時若補零(※詳見5.2.1 Pad with zeros.)，會出現與same效果相等的結果

◎使用Full的效果(框線內是為了跟same做比較)


Page 95
fspecial('average',[5,7])→矩陣的element都是0.286(總和為1)
fspecial('average',11)→矩陣內的element都是0.0083(總和為1)
◎程式碼demo如下(3x3大小的filter)：


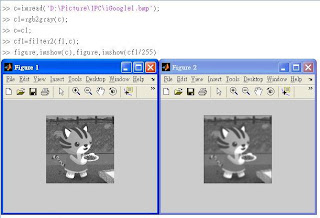
◎同上，改用9x9與25x25的filter：



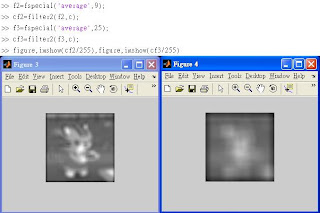
關於Functio "fspecial"，Page 98用到fspecial('')
'laplacian' filter approximating the 2-D Laplacian operator
'log'　　　　Laplacian of Gaussian filter
'gaussian'　Gaussian lowpassfilter
註：laplacian又叫做「拉普拉斯」
◎Page 98的程式結果如下：


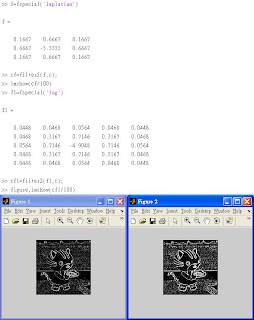
Page 101 =>High-pass filters are often used for edge detction.
◎Page 101-Scaling transformation.

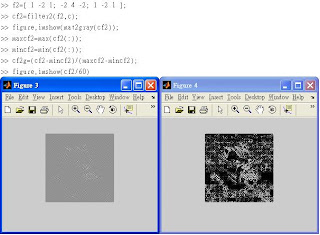
↑據說右邊那個圖，High-pass filters are often used for edge detection. The picture can be seen quite clearly.

※5.5 (未細讀)
關於「Gaussian Filter」
◎但是下圖展示關於Gaussian的效用：


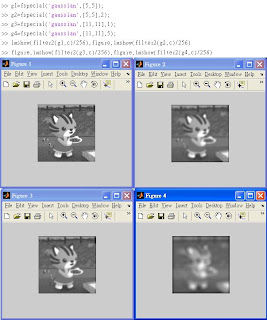
※5.7 Nonlinear Filters
→maximum filter
→minimum filter
→rank-order filter
the mini filter is a rank-order filter for which the first element is returned,and the maximum filter is a rank-order filter for which the last element is returned.

Use function "nlfilter"


※問題區
1.　Page 93,94
　　關於filter2的"same","valid","full"，
　　課本有些簡單的範例，例如在x的四周補0後使用"valid"的效果
　　與直接使用"same"的效果相同
　　知道每個單字出現的範圍大小，但實際計算方式仍不太了解
　　→已知課本範例結果"valid"3×3,"same"5×5,"full"7×7

2.　Page 96,97 5.3.1
　　關於「Separable Filters」
　　示範把陣列分離成1×N與N×1
　　並提到Separability can result in great time savings.
　　關於這邊，語句上的翻譯是節省時間
　　而關於節省，到底是節省怎樣的時間？
　　抑或是節省記憶體的空間呢？(是否有此項功能)

3.　Page 99 Figure 5.5 的解說
　　In each case, the sum of all filter element is zero.
　　意指，構成上述圖片的fliter元素相加總合為0
　　在網路上搜尋了關於Laplacian的事蹟，
　　或許這問題不是很重要，但仍然好奇該矩陣是如何構成？

4.　Page 108 (應該放到課本找錯區嗎= =?)
　　f=[-1 -1 -1;-1 11 -1; -1 -1 -1]/9;
　　xf=filter2(x,f);
　　imswho(xf/80)
　　根據上述指令操作，只有出現一個小點(約3×3大小)
　　但當我將xf=filter2(f,x); //x與f的位置對調
　　就可以show出圖片大小的圖

5.　Page 111(應該放在課本找錯區)
　　假設有一張圖片存在x裡面
　　原本→cmax=nlfilter(c,[3,3],'max(x(:))');會不能用
　　修改→cmax=nlfilter(x,[3,3],'max(x(:))');才能用
　　→cmin亦同
　　但當我將一張圖片大小與x相同的圖片塞到c裡
　　就可以用課本上的指令，那麼該算是筆誤還是？
　　如此一來，是否意指cmax=nlfilter(x,[3,3],'max(x(:))');前後變數該相同？



※專業術語問題區
1.　high-boost filter = 高xx濾波器？
　　同上，high-pass filter = 高xx濾波器？

2.　geometric mean filter

3.　alpha-trimmed mean filter

4.