※7.1 Introduction
[Thinking]
a.為何要使用傅立葉轉換(Fourier Transform)?
b.使用傅立葉轉換有什麼好處?
[Note]
→It is more efficient to use the Fourier transform than a spatial filter for a large filter.
※7.2 Background (背景)
[Thinking]
a.傅立葉的來源背景?
b.為何會發展出傅立葉轉換?
[Note]
→簡單的推導了傅立葉公式
※7.3 The One-Dimensional Discrete Fourier Transform
[Thinking]
a.One-Dimensional的翻譯是一次(階)?
b.假使可翻譯成「一階離散傅立葉轉換」
表示傅立葉轉換可分為 離散、連續、一階、多階等形態?
[Note]
離散傅立葉轉換(Discrete Fourier transform,DFT)
從連續到離散(轉自wiki)
x(t)在時域採樣後的連續富立葉轉換,也就是離散時間富立葉轉換,它在頻域依然是連續的。下面將頻域信號轉化為有限長離散信號。與對時域信號的處理類似,假設頻域信號是帶限的,再經過離散化,即可得到有限長離散信號。依據採樣定理,時域採樣若要能完全重建原信號,頻域信號\hat{x}(\omega)應當帶限於(0,1/T)。由於時域信號時限於[0, L],由採樣定理以及時頻對偶的關係,頻域的採樣間隔應為1/L。
7.4 Properties of the One-Dimensional DEF
function out = cconv(a,b)
Error: Function definitions are not permitted at the prompt or in scripts.
cconv與conv之間的差異(?)
CONV:The resulting vector is length LENGTH(A)+LENGTH(B)-1.
CCONV:見課本Page.153
Page154的運算式結果與Page153 ifft後的結果一樣
IFFT:IFFT(X) is the inverse discrete Fourier transform of X
7.5 The Two-Dimensional DFT
FFT2(X,MROWS,NCOLS) pads matrix X with zeros to size MROWS-by-NCOLS before transforming.
7.6 Fourier Transforms in MATLAB
7.7 Fourier Transforms of Images
照課本打...\囧/
7.8 Filtering in the Frequency Domain
2007年12月12日 星期三
2007年11月27日 星期二
Chapter6 week11
[實做筆記區]
※6.1 Interpolation of Data
Start with a simple problem:suppose we have a collection of four values that we wish to enlarge to eight.
「如何把四個數字擴大八個數字?」
在6.1中一共提到了四個方法,
而Figure6.1與6.2指的是同一種方法...
「Slightly redrawn」 (Page.120)
X1 ~ X4 之間一共有三個間隔,而每個間隔相差的直為1
X'1 ~ X'8 的長度與 X1~X4的長度相等,此外
X'1 ~ X'8之間一共有七個間隔,每個間隔的大小為3/7 也就是0.4286
數學公式如下:X'=1/3(7x-4)
X =1/7(3x'+4)
「Nearest-neighbor interpolation」 (Page.120)
X →X' 挑最近的的點 如6.3所示
X1最近的點:X'1 & X'2 (課本於X'2標空圈)
X2最近的點:X'3 & X'4
X3最近的點:X'5 & X'6
X4最近的點:X'7 & X'8 (課本於X'7標空圈)
「Linear interpolation」 (Page.121)
F-f(X)/λ = f(X2)-f(X1)/1
→F=λf(X2)+(1-λ)f(X1)
註:F是想知道的X'n
λ是以 X1 到 X2 的距離,F距離 X1 佔整段比例的比數
※6.2 Image Interpolation
6.1提到了點與線之間的數值放大(使用線性做範例)
6.2則是一個面的,也就是Image。
Example:將4×4的Image放大到8×8
(x,y)對應到放大後的位置,用下面的公式計算
該公式稱為 bilinear interpolation
f(x',y')=λμf(x+1,y+1)+λ(1-μ)f(x+1,y)
+(1-λ)μf(x,y+1)+(1-λ)(1-μ)f(x,y)
Matlab內有個function叫做 imresize 負責上述提過的處理
語法是:resize(A, k, 'method')
method一共有:'nearest', 'bilinear', 'bicubic' 三種方法
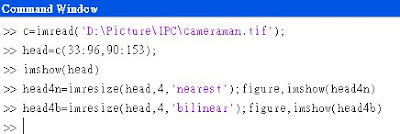
※6.3 General Interpolation (Page.125)
本節提到的是cubic interpolation
也就是Method中的bicubic....
f(x')=R3(-1-λ)f(x1)+R3(-λ)f(x2)+R3(1-λ)f(x3)+R4(2-λ)f(x4)
x'透過 x1, x2, x3, x4 共四個點計算出
解讀如下:
因為計算的過程中該曲線f(x) x值 最高項次是 3次方
此外,在平面上求得(x',y')需仰賴bilinear的概念
故稱為bicubic interpolation
※6.4 Enlargement by Spatial Filtering
在Enlarge的過程中使用filter(?)



※6.5 Scaling Smaller
似乎可以用公式畫圓(但是沒有成功= =)
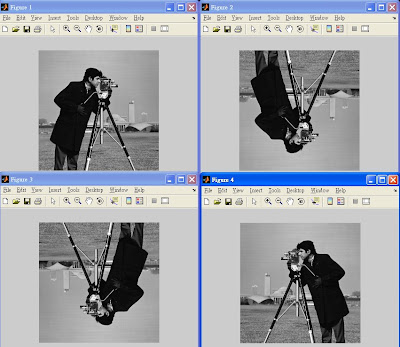
※6.6 Rotation (旋轉)
將圖片(中的每個點)旋轉Θ度
語法如下:var = imrotate(c,60);
//將c旋轉60度的值給var
此外,旋轉90度的倍數有特殊的語法
90度:c90 = flipud(c);
180度:c180 = filplr(flipud(c));
270度:c270 = fliplr(c);

※6.7 Anamorphosis (失真圖像)
[問題區]
1. Page 120, Figure 6.3
Nearest-neighbor interpolation,以空圈標記了最近的點
然而位於邊緣的 X1 ,與 X4 僅僅標記了X'2與X'7
X'1與X'8並未被標,是因為重疊的關係?
在這張圖,從 X'→X 似乎沒有太大的問題
然而從 X→X' 是否如字面意義挑最近的點
例如 X'3 較 X'4更接近 X2...X→X'時,X2是否取X'3的值
2. Page 137
90度:c90 = flipud(c);
180度:c180 = filplr(flipud(c));
270度:c270 = fliplr(c);
因為課本上使用imrotate的旋轉,是逆時鐘旋轉...
然而這邊提到特殊與法的時候,有提到度數
我以為c90的結果應該與imrotate(c,90)相同
然而實際上並不是,而是往下折(x,y')
c180 也不等於 imrotate(c,180)而是(x',y')
c270 是(x',y)
註:(x,y')是指 x 相對位置不變,y的位置作映射
(x',y') x y 作映射
(x',y)是指 y 相對位置不變,x的位置作映射
這樣算是我解讀上有所問題嗎?
※6.1 Interpolation of Data
Start with a simple problem:suppose we have a collection of four values that we wish to enlarge to eight.
「如何把四個數字擴大八個數字?」
在6.1中一共提到了四個方法,
而Figure6.1與6.2指的是同一種方法...
「Slightly redrawn」 (Page.120)
X1 ~ X4 之間一共有三個間隔,而每個間隔相差的直為1
X'1 ~ X'8 的長度與 X1~X4的長度相等,此外
X'1 ~ X'8之間一共有七個間隔,每個間隔的大小為3/7 也就是0.4286
數學公式如下:X'=1/3(7x-4)
X =1/7(3x'+4)
「Nearest-neighbor interpolation」 (Page.120)
X →X' 挑最近的的點 如6.3所示
X1最近的點:X'1 & X'2 (課本於X'2標空圈)
X2最近的點:X'3 & X'4
X3最近的點:X'5 & X'6
X4最近的點:X'7 & X'8 (課本於X'7標空圈)
「Linear interpolation」 (Page.121)
F-f(X)/λ = f(X2)-f(X1)/1
→F=λf(X2)+(1-λ)f(X1)
註:F是想知道的X'n
λ是以 X1 到 X2 的距離,F距離 X1 佔整段比例的比數
※6.2 Image Interpolation
6.1提到了點與線之間的數值放大(使用線性做範例)
6.2則是一個面的,也就是Image。
Example:將4×4的Image放大到8×8
(x,y)對應到放大後的位置,用下面的公式計算
該公式稱為 bilinear interpolation
f(x',y')=λμf(x+1,y+1)+λ(1-μ)f(x+1,y)
+(1-λ)μf(x,y+1)+(1-λ)(1-μ)f(x,y)
Matlab內有個function叫做 imresize 負責上述提過的處理
語法是:resize(A, k, 'method')
method一共有:'nearest', 'bilinear', 'bicubic' 三種方法

※6.3 General Interpolation (Page.125)
本節提到的是cubic interpolation
也就是Method中的bicubic....
f(x')=R3(-1-λ)f(x1)+R3(-λ)f(x2)+R3(1-λ)f(x3)+R4(2-λ)f(x4)
x'透過 x1, x2, x3, x4 共四個點計算出
解讀如下:
因為計算的過程中該曲線f(x) x值 最高項次是 3次方
此外,在平面上求得(x',y')需仰賴bilinear的概念
故稱為bicubic interpolation
※6.4 Enlargement by Spatial Filtering
在Enlarge的過程中使用filter(?)



※6.5 Scaling Smaller
似乎可以用公式畫圓(但是沒有成功= =)
※6.6 Rotation (旋轉)
將圖片(中的每個點)旋轉Θ度
語法如下:var = imrotate(c,60);
//將c旋轉60度的值給var
此外,旋轉90度的倍數有特殊的語法
90度:c90 = flipud(c);
180度:c180 = filplr(flipud(c));
270度:c270 = fliplr(c);


※6.7 Anamorphosis (失真圖像)
[問題區]
1. Page 120, Figure 6.3
Nearest-neighbor interpolation,以空圈標記了最近的點
然而位於邊緣的 X1 ,與 X4 僅僅標記了X'2與X'7
X'1與X'8並未被標,是因為重疊的關係?
在這張圖,從 X'→X 似乎沒有太大的問題
然而從 X→X' 是否如字面意義挑最近的點
例如 X'3 較 X'4更接近 X2...X→X'時,X2是否取X'3的值
2. Page 137
90度:c90 = flipud(c);
180度:c180 = filplr(flipud(c));
270度:c270 = fliplr(c);
因為課本上使用imrotate的旋轉,是逆時鐘旋轉...
然而這邊提到特殊與法的時候,有提到度數
我以為c90的結果應該與imrotate(c,90)相同
然而實際上並不是,而是往下折(x,y')
c180 也不等於 imrotate(c,180)而是(x',y')
c270 是(x',y)
註:(x,y')是指 x 相對位置不變,y的位置作映射
(x',y') x y 作映射
(x',y)是指 y 相對位置不變,x的位置作映射
這樣算是我解讀上有所問題嗎?
2007年11月25日 星期日
期中報告 notes
3. [ 注意 ] 請同學撰寫一份期中報告, 繳交至 Homework Show @ IPC, 內容為描述自己在本課程前半學期的學習情形, 回顧自己哪方面表現不錯? 哪方面需要加強? 老師應加強哪些課程內容? 最後, 給自己的學習打成績。第 11 週課程我們將進行課程期中回顧。
筆記筆記筆記....囧
待續XD
[學習情形]
每週都有按照老師規定的進度好好的閱讀與實做
除了3.6(如果沒記錯)那次沒有跟上外
[自認不錯]
有試著使用blog做閱讀紀錄,
方便將來回顧時使用。
[尚待加強]
上課學過的東西,或許當下聽懂了,
然而有部分機率在不久後將之遺忘。
[課程內容]
本身對於課程內容與上課方式並沒有任何疑問
[自我評分]
80
雖然有使用blog做紀錄,然而紀錄卻不是那麼的詳細
有時因為偷懶而缺記的,還得重新翻書才會有印象
提問題,總覺得有一些是可以自行解決的...
提問題之後,或得解答也未必即時更新blog
有時問題提過後,部份沒獲得解答的問題就此閒置
就努力實作與閱讀方面,覺得應該有超過80分的門檻
但是因為後續偷懶方面的小瑕疵,自認該扣分...
筆記筆記筆記....囧
待續XD
[學習情形]
每週都有按照老師規定的進度好好的閱讀與實做
除了3.6(如果沒記錯)那次沒有跟上外
[自認不錯]
有試著使用blog做閱讀紀錄,
方便將來回顧時使用。
[尚待加強]
上課學過的東西,或許當下聽懂了,
然而有部分機率在不久後將之遺忘。
[課程內容]
本身對於課程內容與上課方式並沒有任何疑問
[自我評分]
80
雖然有使用blog做紀錄,然而紀錄卻不是那麼的詳細
有時因為偷懶而缺記的,還得重新翻書才會有印象
提問題,總覺得有一些是可以自行解決的...
提問題之後,或得解答也未必即時更新blog
有時問題提過後,部份沒獲得解答的問題就此閒置
就努力實作與閱讀方面,覺得應該有超過80分的門檻
但是因為後續偷懶方面的小瑕疵,自認該扣分...
2007年11月6日 星期二
Week7 Homework7
※閱讀心得--以下以章節與頁數呈現
※5.1 Introduction
[Page 89]
Spatial filtering thus requires three steps:
1. Position the mask over the current pixel.
2. Form all products of filter elements with the corresponding elements of the neighborhood.
3. Add all the products.
↑This must be repeated for pixel in the image. (!!!!)
關於我的解讀:
1. 先選出想要的current pixel
2. 列出他的Pixel Neighborhood
3. 選定他是Mask的範圍
4. 將週遭的Neighborhood乘上特定乘積並加總在current pixel的位置
5. 輸出
[Page 90]
magic(N)就是楊建貴教授以前敎過的魔術方塊
N是決定他的大小:N×N大小的矩陣

↑分別是乘以10之後與之前
課本將之乘以10倍的大小
關於Page 90與Page 91的程式範例,有誤導的錯覺
因此自製了一些對照圖:



※5.3 Filtering in MATLAB
Y = filter2(B,X,'shape')
'same'-原本的大小 (原本是5×5的話)
'valid'-compute without the zero-padded(會變3×3)
'full'- 把邊緣也用特殊算法填滿(7×7)
使用圖片對照應該會更加清晰,如下:
◎使用same
 ◎使用valid
◎使用valid

◎使用valid時若補零(※詳見5.2.1 Pad with zeros.),會出現與same效果相等的結果

◎使用Full的效果(框線內是為了跟same做比較)

Page 95
fspecial('average',[5,7])→矩陣的element都是0.286(總和為1)
fspecial('average',11)→矩陣內的element都是0.0083(總和為1)
◎程式碼demo如下(3x3大小的filter):
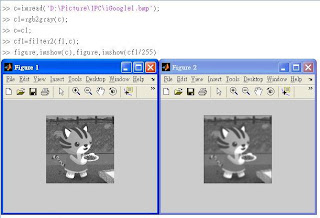
◎同上,改用9x9與25x25的filter:
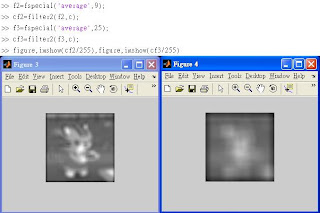
關於Functio "fspecial",Page 98用到fspecial('')
'laplacian' filter approximating the 2-D Laplacian operator
'log' Laplacian of Gaussian filter
'gaussian' Gaussian lowpassfilter
註:laplacian又叫做「拉普拉斯」
◎Page 98的程式結果如下:
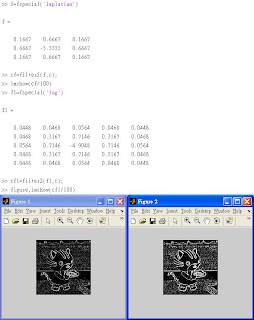
Page 101 =>High-pass filters are often used for edge detction.
◎Page 101-Scaling transformation.
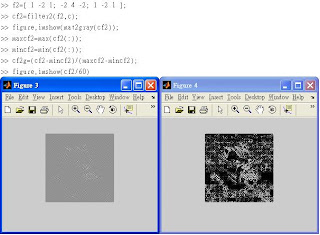
↑據說右邊那個圖,High-pass filters are often used for edge detection. The picture can be seen quite clearly.
※5.5 (未細讀)
關於「Gaussian Filter」
◎但是下圖展示關於Gaussian的效用:
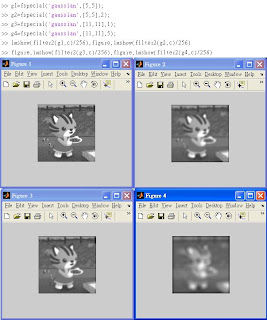
※5.7 Nonlinear Filters
→maximum filter
→minimum filter
→rank-order filter
the mini filter is a rank-order filter for which the first element is returned,and the maximum filter is a rank-order filter for which the last element is returned.
Use function "nlfilter"
※問題區
1. Page 93,94
關於filter2的"same","valid","full",
課本有些簡單的範例,例如在x的四周補0後使用"valid"的效果
與直接使用"same"的效果相同
知道每個單字出現的範圍大小,但實際計算方式仍不太了解
→已知課本範例結果"valid"3×3,"same"5×5,"full"7×7
2. Page 96,97 5.3.1
關於「Separable Filters」
示範把陣列分離成1×N與N×1
並提到Separability can result in great time savings.
關於這邊,語句上的翻譯是節省時間
而關於節省,到底是節省怎樣的時間?
抑或是節省記憶體的空間呢?(是否有此項功能)
3. Page 99 Figure 5.5 的解說
In each case, the sum of all filter element is zero.
意指,構成上述圖片的fliter元素相加總合為0
在網路上搜尋了關於Laplacian的事蹟,
或許這問題不是很重要,但仍然好奇該矩陣是如何構成?
4. Page 108 (應該放到課本找錯區嗎= =?)
f=[-1 -1 -1;-1 11 -1; -1 -1 -1]/9;
xf=filter2(x,f);
imswho(xf/80)
根據上述指令操作,只有出現一個小點(約3×3大小)
但當我將xf=filter2(f,x); //x與f的位置對調
就可以show出圖片大小的圖
5. Page 111(應該放在課本找錯區)
假設有一張圖片存在x裡面
原本→cmax=nlfilter(c,[3,3],'max(x(:))');會不能用
修改→cmax=nlfilter(x,[3,3],'max(x(:))');才能用
→cmin亦同
但當我將一張圖片大小與x相同的圖片塞到c裡
就可以用課本上的指令,那麼該算是筆誤還是?
如此一來,是否意指cmax=nlfilter(x,[3,3],'max(x(:))');前後變數該相同?
※專業術語問題區
1. high-boost filter = 高xx濾波器?
同上,high-pass filter = 高xx濾波器?
2. geometric mean filter
3. alpha-trimmed mean filter
4.
※5.1 Introduction
[Page 89]
Spatial filtering thus requires three steps:
1. Position the mask over the current pixel.
2. Form all products of filter elements with the corresponding elements of the neighborhood.
3. Add all the products.
↑This must be repeated for pixel in the image. (!!!!)
關於我的解讀:
1. 先選出想要的current pixel
2. 列出他的Pixel Neighborhood
3. 選定他是Mask的範圍
4. 將週遭的Neighborhood乘上特定乘積並加總在current pixel的位置
5. 輸出
[Page 90]
magic(N)就是楊建貴教授以前敎過的魔術方塊
N是決定他的大小:N×N大小的矩陣

↑分別是乘以10之後與之前
課本將之乘以10倍的大小
關於Page 90與Page 91的程式範例,有誤導的錯覺
因此自製了一些對照圖:



※5.3 Filtering in MATLAB
Y = filter2(B,X,'shape')
'same'-原本的大小 (原本是5×5的話)
'valid'-compute without the zero-padded(會變3×3)
'full'- 把邊緣也用特殊算法填滿(7×7)
使用圖片對照應該會更加清晰,如下:
◎使用same
 ◎使用valid
◎使用valid
◎使用valid時若補零(※詳見5.2.1 Pad with zeros.),會出現與same效果相等的結果

◎使用Full的效果(框線內是為了跟same做比較)

Page 95
fspecial('average',[5,7])→矩陣的element都是0.286(總和為1)
fspecial('average',11)→矩陣內的element都是0.0083(總和為1)
◎程式碼demo如下(3x3大小的filter):

◎同上,改用9x9與25x25的filter:

關於Functio "fspecial",Page 98用到fspecial('')
'laplacian' filter approximating the 2-D Laplacian operator
'log' Laplacian of Gaussian filter
'gaussian' Gaussian lowpassfilter
註:laplacian又叫做「拉普拉斯」
◎Page 98的程式結果如下:

Page 101 =>High-pass filters are often used for edge detction.
◎Page 101-Scaling transformation.

↑據說右邊那個圖,High-pass filters are often used for edge detection. The picture can be seen quite clearly.
※5.5 (未細讀)
關於「Gaussian Filter」
◎但是下圖展示關於Gaussian的效用:

※5.7 Nonlinear Filters
→maximum filter
→minimum filter
→rank-order filter
the mini filter is a rank-order filter for which the first element is returned,and the maximum filter is a rank-order filter for which the last element is returned.
Use function "nlfilter"
※問題區
1. Page 93,94
關於filter2的"same","valid","full",
課本有些簡單的範例,例如在x的四周補0後使用"valid"的效果
與直接使用"same"的效果相同
知道每個單字出現的範圍大小,但實際計算方式仍不太了解
→已知課本範例結果"valid"3×3,"same"5×5,"full"7×7
2. Page 96,97 5.3.1
關於「Separable Filters」
示範把陣列分離成1×N與N×1
並提到Separability can result in great time savings.
關於這邊,語句上的翻譯是節省時間
而關於節省,到底是節省怎樣的時間?
抑或是節省記憶體的空間呢?(是否有此項功能)
3. Page 99 Figure 5.5 的解說
In each case, the sum of all filter element is zero.
意指,構成上述圖片的fliter元素相加總合為0
在網路上搜尋了關於Laplacian的事蹟,
或許這問題不是很重要,但仍然好奇該矩陣是如何構成?
4. Page 108 (應該放到課本找錯區嗎= =?)
f=[-1 -1 -1;-1 11 -1; -1 -1 -1]/9;
xf=filter2(x,f);
imswho(xf/80)
根據上述指令操作,只有出現一個小點(約3×3大小)
但當我將xf=filter2(f,x); //x與f的位置對調
就可以show出圖片大小的圖
5. Page 111(應該放在課本找錯區)
假設有一張圖片存在x裡面
原本→cmax=nlfilter(c,[3,3],'max(x(:))');會不能用
修改→cmax=nlfilter(x,[3,3],'max(x(:))');才能用
→cmin亦同
但當我將一張圖片大小與x相同的圖片塞到c裡
就可以用課本上的指令,那麼該算是筆誤還是?
如此一來,是否意指cmax=nlfilter(x,[3,3],'max(x(:))');前後變數該相同?
※專業術語問題區
1. high-boost filter = 高xx濾波器?
同上,high-pass filter = 高xx濾波器?
2. geometric mean filter
3. alpha-trimmed mean filter
4.
2007年10月31日 星期三
Week6 Homework6
※Chapter 4 閱讀與實作心得與提問
4.1 Introduction
關於影像處理的運算,大約可以分成三種類型
1.Transforms.(轉換)
Figure 4.1 show了圖片處理的四個步驟:
Image→Transformed image→Processed transformed image
→Processed original image
2.Neighborhood processing(鄰近範圍的處理)
改變一張灰階圖片的Level,需要參照其他Pixel的Level。
3.Point operations.(點的運算)
特定的Pixel改變時,不影響其他的Pixels。
4.2 Arithmetic Operations(算術運算)
令整張圖片當作一個f(x)函數,使用數學上的運算處理。
Figure 4.2,左圖是將所有的Pixels都增加128..
如此一來,value高於128的會在相加後超過255。 (右圖則是減去128)
此外,稍稍的提到了immultiply(乘)與imdivide(除) function
COMPLEMENTS
課本上提到了bc=imcomplement(b);
bc是b這張圖片(矩陣)的補數
show出來的圖片會有solarization(曝曬作用)的效果 //<-Question!!
4.3 Histograms
一個灰階的圖片,統計gray level後可以將每個level所擁有的值繪致成一張長條圖(Histogram)。而關於這個長條圖(Histogram)擁有以下幾點特點:
˙在顏色深一點的圖片,gray level大多分布聚集在較低的level中
˙在顏色亮一點的圖片,gray level大多分布聚集在較高的level中
˙在對比良好的圖片中,gray level會平均分布在全部level中
4.3.1 Page74~75
關於plot(t,th,'.'),axis tight
我試著打出plot(t,t,'.'), plot(th,th,'.'), plot(th,t,'.')
當變數相等時,由點構成 y=x 的線
→plot(x,y) 由x值範圍當x軸,y值範圍當y軸
而關於imadjust(t,[],[],0.5); //0.5即gamma value
我試過imadjust(t,[0~1 0~1],[])
雖然有看出圖片的不同,但想不出該如何解釋現象//Question!!
4.3.2 Histogram Equalization(均化作用)
說到Histogram的均化,大概可以分成兩種:
1.讓每個bar都有一樣的高度
2.讓每個gray level出現的頻率相同
課本的均化作用似乎偏向於2...
「使Histogram平均分布在255個level中」
Page.78 定義一個n=360,把它分成15層→15/360= 1/24
Figure 4.17原本的level在均化後以Figure4.18呈現
但是...Histogram的bar竟然少一條!! //Question!!!
4.4 Lookup Tables(查表法)
Page.83的Commands是在實現 Figure 4.23
t1=0.6667*[0:64];
t2=2*[65:160]-128;
t3=0..6632*[161:255]+85.8947;
T=uint8(floor([t1 t2 t3]));
解讀如下:
T是user所建立的一個table
當gray image的pixel value是從
0~64時,對照 t1的算式→new value
65~160,對照t2的算式→new value
161~255,對照t3的算式→new value
※問題區(將上述問題特別整理出來)
1.COMPLEMENTS
使用imcomplement指令,會產生元圖片的補數
而補數show成一張image時會有曝曬作用的效果
(以上我根據課本內容所做出來的解讀)
→照片的負片是否與這個作用有關?(關於舊式底片的問題)
→所謂的曝曬作用,是指圖片嚴重曝光嗎?
2.imadjust 我試過imadjust(t,[0~1 0~1],[])
雖然有看出圖片的不同,但想不出該如何解釋現象
3.Histogram Equalization
Page.78 定義一個n=360,把它分成15層→15/360= 1/24
Figure 4.17原本的level在均化後以Figure4.18呈現
但是...Histogram的bar竟然少一條!!
我反覆推算,還是想不出那條bar到底落到哪區
以上是我重新閱讀與思索第四章後的心得筆記問題
有部分與上週產生的問題重複,有部分已經解決....
4.1 Introduction
關於影像處理的運算,大約可以分成三種類型
1.Transforms.(轉換)
Figure 4.1 show了圖片處理的四個步驟:
Image→Transformed image→Processed transformed image
→Processed original image
2.Neighborhood processing(鄰近範圍的處理)
改變一張灰階圖片的Level,需要參照其他Pixel的Level。
3.Point operations.(點的運算)
特定的Pixel改變時,不影響其他的Pixels。
4.2 Arithmetic Operations(算術運算)
令整張圖片當作一個f(x)函數,使用數學上的運算處理。
Figure 4.2,左圖是將所有的Pixels都增加128..
如此一來,value高於128的會在相加後超過255。 (右圖則是減去128)
此外,稍稍的提到了immultiply(乘)與imdivide(除) function
COMPLEMENTS
課本上提到了bc=imcomplement(b);
bc是b這張圖片(矩陣)的補數
show出來的圖片會有solarization(曝曬作用)的效果 //<-Question!!
4.3 Histograms
一個灰階的圖片,統計gray level後可以將每個level所擁有的值繪致成一張長條圖(Histogram)。而關於這個長條圖(Histogram)擁有以下幾點特點:
˙在顏色深一點的圖片,gray level大多分布聚集在較低的level中
˙在顏色亮一點的圖片,gray level大多分布聚集在較高的level中
˙在對比良好的圖片中,gray level會平均分布在全部level中
4.3.1 Page74~75
關於plot(t,th,'.'),axis tight
我試著打出plot(t,t,'.'), plot(th,th,'.'), plot(th,t,'.')
當變數相等時,由點構成 y=x 的線
→plot(x,y) 由x值範圍當x軸,y值範圍當y軸
而關於imadjust(t,[],[],0.5); //0.5即gamma value
我試過imadjust(t,[0~1 0~1],[])
雖然有看出圖片的不同,但想不出該如何解釋現象//Question!!
4.3.2 Histogram Equalization(均化作用)
說到Histogram的均化,大概可以分成兩種:
1.讓每個bar都有一樣的高度
2.讓每個gray level出現的頻率相同
課本的均化作用似乎偏向於2...
「使Histogram平均分布在255個level中」
Page.78 定義一個n=360,把它分成15層→15/360= 1/24
Figure 4.17原本的level在均化後以Figure4.18呈現
但是...Histogram的bar竟然少一條!! //Question!!!
4.4 Lookup Tables(查表法)
Page.83的Commands是在實現 Figure 4.23
t1=0.6667*[0:64];
t2=2*[65:160]-128;
t3=0..6632*[161:255]+85.8947;
T=uint8(floor([t1 t2 t3]));
解讀如下:
T是user所建立的一個table
當gray image的pixel value是從
0~64時,對照 t1的算式→new value
65~160,對照t2的算式→new value
161~255,對照t3的算式→new value
※問題區(將上述問題特別整理出來)
1.COMPLEMENTS
使用imcomplement指令,會產生元圖片的補數
而補數show成一張image時會有曝曬作用的效果
(以上我根據課本內容所做出來的解讀)
→照片的負片是否與這個作用有關?(關於舊式底片的問題)
→所謂的曝曬作用,是指圖片嚴重曝光嗎?
2.imadjust 我試過imadjust(t,[0~1 0~1],[])
雖然有看出圖片的不同,但想不出該如何解釋現象
3.Histogram Equalization
Page.78 定義一個n=360,把它分成15層→15/360= 1/24
Figure 4.17原本的level在均化後以Figure4.18呈現
但是...Histogram的bar竟然少一條!!
我反覆推算,還是想不出那條bar到底落到哪區
以上是我重新閱讀與思索第四章後的心得筆記問題
有部分與上週產生的問題重複,有部分已經解決....
2007年10月19日 星期五
Week5 Homework5
[Notes]
※4.1 Introduction
Image-processing operations may be divided into three classes based on the information required to perform the transformation.
1.Transforms.
2.Neighborhood processing.
3.Point operation.
※4.2 Arithmetic Operations
※4.3 Histograms
→imshow(p),figure,imhist(p),axis tight
├4.3.1 Histogram Stretching
│ gamma value(?)
└4.3.2 Histogram Equalization
qualization
※4.4 Lookup Tables
Questions:
1.LUT(?)
※4.1 Introduction
Image-processing operations may be divided into three classes based on the information required to perform the transformation.
1.Transforms.
2.Neighborhood processing.
3.Point operation.
※4.2 Arithmetic Operations
※4.3 Histograms
→imshow(p),figure,imhist(p),axis tight
├4.3.1 Histogram Stretching
│ gamma value(?)
└4.3.2 Histogram Equalization
qualization
※4.4 Lookup Tables
Questions:
1.LUT(?)
2007年10月17日 星期三
Week4 Homework4
閱讀3.6 Quantization and Dithering
[Notes]
uint8(floor(double(x)/2)*2)...etc
imshow(grayslice(x,128),gray(128)) <=分成幾層灰階的色階 Dither 的中文解釋(?) Questions: 1.Dithering Dither: a.[to be unable to make a decision about doing something] verb b.[be in a dither about sth to be very nervous, excited or confused about something] noun 不知道在IPC中,Dither該如何翻譯 2.承上 Page.56~57 關於矩陣D=[ 0 128; 192 64 ]那方面,我的解讀是將圖片切割成N個以2*2為一個blog做單位,逐一與D比較,會因為資料數據而簡單將區塊劃分為「Dark gray」、「Midgray」、「Light gray」如同Figure 3.13的顯示。而我發現Figure 3.14並不是完全的純黑白數據而已,於是翻看Page.57程式碼部分,由於x2=x>r ,imshow(x2) 所產生的Figure 3.14仍有色差,這點很不能理解。
3.承一,希望更詳細理解Dithering的意義,有點不能理解Page.61圖片參雜著雜訊點的意義。
[Notes]
uint8(floor(double(x)/2)*2)...etc
imshow(grayslice(x,128),gray(128)) <=分成幾層灰階的色階 Dither 的中文解釋(?) Questions: 1.Dithering Dither: a.[to be unable to make a decision about doing something] verb b.[be in a dither about sth to be very nervous, excited or confused about something] noun 不知道在IPC中,Dither該如何翻譯 2.承上 Page.56~57 關於矩陣D=[ 0 128; 192 64 ]那方面,我的解讀是將圖片切割成N個以2*2為一個blog做單位,逐一與D比較,會因為資料數據而簡單將區塊劃分為「Dark gray」、「Midgray」、「Light gray」如同Figure 3.13的顯示。而我發現Figure 3.14並不是完全的純黑白數據而已,於是翻看Page.57程式碼部分,由於x2=x>r ,imshow(x2) 所產生的Figure 3.14仍有色差,這點很不能理解。
3.承一,希望更詳細理解Dithering的意義,有點不能理解Page.61圖片參雜著雜訊點的意義。
訂閱:
意見 (Atom)